My Current Research Topic: Many-Body Localisation
It’s always exciting in science when a surprise comes along and something you thought you knew turns out to be wrong. In the last decade, spurred on by recent experimental advances, condensed matter theorists have turned back to an old problem with renewed enthusiasm, and have discovered an enigmatic phase of matter that behaves unlike anything else we know of.
The behaviour in question is called many-body localisation and it’s the topic of my current research. The problem has its historical origins in a theoretical model that we now call the Anderson model. It’s a mathematical model that describes electrons moving around in a disordered crystal independently of one another, without any interactions between them.
You can imagine building this sort of material by starting with a regular bit of metal and adding enough impurities into it that the electrons can’t move – they become stuck in place, or localised. If the electrons can’t move, the material can’t conduct and so it becomes an insulator. These impurities could be, say, extra atoms crammed into the gaps between existing atoms, or could come from replacing atoms in the metal with atoms of a different type, or essentially anything else you can think of that doesn’t destroy the crystal structure of the material.
It turns out that any amount of disorder in this model, no matter how small, is enough to prevent very thin wires from conducting. This is essentially because any impurity in a wire is like a blockage in a pipe – there’s nowhere for the fluid (current) to go, so it gets stuck and the material can’t conduct. The water can still circulate in the regions between blockages – we call the average length between blockages the ‘localisation length’ – but provided the pipe contains one or more blockages, the water can’t flow from one end to the other.
Although the idea of the electrons not interacting with each other seems a little abstract, nowadays it really is possible to engineer such materials in real experiments. The advent of this level of experimental control over quantum systems led to renewed interest in the idea of localisation in quantum systems, and in particular what would happen if interactions were added. The suspicion was that once the electrons are able to interact with each other they would be able to quantum-tunnel straight through the blockages as if they weren’t there, allowing the electrons to once more roam freely through the wire, rendering the material conducting once more.
There were many good reasons to believe that this was true, but it wasn’t until 2006 that the question was finally formulated in a mathematical way that theorists could attempt to answer rigorously. The answer turned out to be surprising – even after turning on the interactions that should allow the electrons to move freely, for strong enough disorder they remain localised and the wires stay insulating.
If that were the end of the story, it wouldn’t be a big deal. By adding impurities into a metal, we stop it being a metal – big deal, right? Turns out, there’s a little more to it.
Turning on interactions in this system doesn’t give us back a regular insulator of the type that we were familiar with already. In fact, it gives us a new phase of matter we call the many-body localised phase which behaves very differently to almost every other phase of matter.
Left to their own devices, most physical systems reach a thermal equilibrium with their environment. Think of a Newton’s Cradle – you give it energy to set it moving, but eventually that energy gets dissipated through heat and sound and eventually the pendulums stop. Likewise, if you put a hot cup of coffee in a cold room, the coffee will give up its heat until it ends up at the same temperature as the room. We call this equilibration or thermalisation.
Most interacting materials thermalise, but many-body localised (MBL) phases don’t. An MBL material can’t reach a thermal equilibrium with its surroundings, or even with itself – it gets stuck in what we call a highly excited state, where the material is unable to dissipate energy within itself and thermalise. MBL materials are therefore perfect insulators of both electricity and heat.
In fact, even the idea of temperature stops being meaningful in an MBL phase – does a single electron have a temperature? Do two? We can only start talking about things like temperature when we have enough particles to start treating them statistically, but in an MBL system, the wire becomes fragmented into very small regions (each containing only a few particles) that are essentially completely cut off from each other and unable to communicate in any way. (These regions are known as ‘localised bits’ (l-bits) or ‘local integrals of motion’ (LIOMs).)
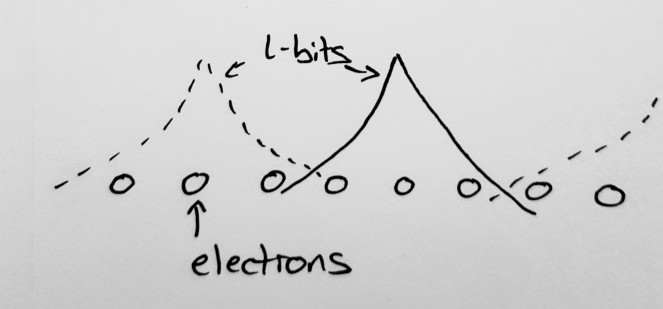
Any image of how quantum particles behave will be wrong, but for what it’s worth this is kind of how I picture l-bits: small regions of electrons that bunch together into composite particles known as l-bits, which have only a small ‘overlap’ with the other l-bits nearby to them. YMMV.
Because the material has no way to dissipate energy, it essentially keeps a memory of its initial state – imagine setting a Newton’s cradle going and it staying at the same speed forever, instead of dissipating that energy to its environment and slowing down. This means that unlike in a typical quantum system, information written into an MBL phase will persist indefinitely, making them potentially useful for quantum computing and storage applications. Perhaps even more interestingly, if the idea of temperature doesn’t mean anything to these materials, then expense and effort of cooling them to cryogenic temperatures is no longer necessary. MBL could be a mechanism by which we can protect genuine quantum mechanical behaviour in materials at temperatures high enough to be practical for future technologies.
That said, our understanding of MBL is still in its infancy and many significant questions remain. To really understand it, to figure out how it works, to harness its effects and design new materials to take advantage of them, we need to go beyond the standard theorist’s toolkit. We need new techniques, new ideas.
Equilibrium quantum statistical mechanics, laid down in the early days of quantum mechanics by the giants of the field and built on by virtually all those who came after, just doesn’t cut it any more. We need to go beyond this paradigm, into new physics where we combine strongly interacting quantum many-body systems with the study of randomness and disorder, then we need to go further still into the physics of non-equilibrium. Each of these is a difficult problem – taken together, things get really interesting.
Watch this space. 😉
