Spinning out of Equilibrium
When ice melts in a drink or a cup of coffee cools down to room temperature, energy is exchanged between the drink and its environment until they reach a thermal equilibrium. This is true for any physical system, from regular liquids like drinks through to complex quantum mechanical systems like trapped ions or ultracold atomic gases. When a system connected to its environment is subject to some form of perturbation, it will always eventually return back to its equilibrium state: think of a Newton’s cradle, for example, which you can ‘perturb’ by setting it in motion, but which will always eventually return to its equilibrium (static) state as its kinetic energy is slowly dissipated to its environment through friction (heat) and sound.
One exception to this rule is if the physical system has some built-in defects or randonmess that inhibit thermalisation, such as in the case of spin glasses and other so-called ‘glassy’ phases like liquid crystals and colloids, where the return to an equilibrium state is extremely slow. This means that for most practical purposes, glassy systems never return to an equilibrium state. The name comes from an analogy with typical window glass, where structural disorder prevents the atoms from forming a crysalline lattice, although in the following we will be more concerned with magnetic disorder rather than structural disorder. The name is also reminisent of the (false) idea that glass is essentially a ‘slow liquid’ - you may have heard the myth that the stained glass windows in old churches are thicker near the bottom, due to the glass slowly flowing down under the pull of gravity. This isn’t true, but it illustrates the point: glassy systems react extremely slowly, even when able to exchange energy with their environments.
But what happens to isolated quantum glasses, unable to exchange energy with their environment, when they are perturbed away from equilibrium? In a recent work published in Physical Review Letters, my co-workers and I have attempted to answer this question.

What’s the problem?
Isolated quantum systems, by definition, cannot exchange energy with their environment: they are completely cut off from the rest of the world. The only way an isolated system can thermalise is within itself, via interactions between different parts of the system. For example, imagine again dropping an ice cube in a drink, but this time imagine the rest of the universe doesn’t exist. What would happen?
Well, in this case the ice cube will still melt, and lower the temperature of the drink, but it will never reach `room temperature'. The final temperature of the drink will be entirely determined by the initial temperature of the drink and the ice cube - but not uniquely. If the drink is cold, it may be because a large ice cube was added to a warm drink, or a small ice cube added to a cold drink. In other words, it may not be possible to uniquely determine what the initial state was, and for all intents and purposes that information is lost to us if the system thermalises, even within itself.
Thermalisation is information loss, in other words - while the information about the initial state is strictly still present, it is all but impossible to recover.
So, the question we wanted to ask is “Can quantum glasses isolated from their environment retain a ‘memory’ of their initial conditions?” - but before getting to that, why do we even care?
Why is this important/interesting?
Understanding how physical systems thermalise, or fail to do so, is important both from a fundamental standpoint, and from the point of view of developing future quantum technologies. Instead of an ice cube and a drink, now imagine that we’re using a quantum computer and trying to write data to a quantum bit (qubit). It’s vitally important in this case that the qubit ‘remember’ the data written to it: in other words, it’s important that the qubit does not thermalise so that it retains a memory of its initial conditions. If the qubit were to thermalise, then like the melting ice cube, all information contained in it would effectively be lost. Thermalisation is a serious problem for quantum technologies, and preventing thermalisation is a key goal in realising practical quantum technologies of the future.
One method of preventing quantum systems from thermalising - and from my point of view the most interesting one! - is the addition of disorder into the system. This can take many forms, from chemical impurities in sold-state systems through to speckle patterns of light in ultracold atomic gases. Disorder is an important ingredient in spin glasses, where the high degree of randomness makes it immensely difficult for the system to reach a thermal equilibrium. The underlying physics of spin glasses comes from classical - i.e. not quantum - physics, but quantum fluctuations in spin glasses tend to speed up the thermalisation process, shortening their memory. However, with recent discoveries in the field of many-body localisation showing that quantum effects can completely prevent thermalisation in a certain class of systems, we noticed that no one had ever investigated the thermalisation properties of quantum spin glasses when isolated from their environments. While our intuition based on previous spin glass studies was that quantum fluctuations would indeed shorten the memory of the system, the developments in many-body localisation suggested the interesting possibility that quantum effects might do the opposite, and stabilise spin glass order, allowing the system to retain a memory for much longer times than the equivalent system connected to an environment. So with that in mind…
What exactly did we study?
We’re interested in more exotic forms of quantum matter than drinks and ice cubes, mostly centred around ultracold atomic gases and trapped ions as these are potential platforms for quantum computing, and in particular we theoretically investigated a model known as the p-spin model. This (admittedly rather abstract) mathematical model describes a series of quantum spins all connected to each other with random couplings. The model contains two main adjustable parameters, namely the temperature \(T \) and the strength of quantum fluctuations (typically denoted \( \Gamma = \hbar^2/J m\) in the notation of the model). It’s known as a ‘mean field’ model of a spin glass, because it can be exactly solved using mean-field (read: relatively simple) techniques.
A sketch of the spatial structure of a p-spin model, where every quantum spin (black dots) is connected to every other quantum spin (blue lines).
The p-spin model contains two phases, known as paramagnetic and spin glass phases. The paramagnetic phase exists at high temperatures and/or strong quantum fluctuations, whereas the spin glass exists at low temperatures and/or weak quantum fluctuations. It turns out that despite the abstraction, this model qualitatively reproduces the behaviour seen in a wide range of materials. This model has been extensively studied in the past, notably by Leticia Cugliandolo and co-workers, as well as more recently by Chris Laumann and others in the context of many-body localisation.

A phase diagram of the p-spin model, showing the spin glass phase (SG, in blue) that exists at low temperatures T and small values of quantum fluctuations.
Our main aim was to take the p-spin model, isolated from its environment, and see how it relaxes back to equilibrium following a sudden parameter change (known as a quantum quench), a bit like setting a Newton’s cradle in motion or dropping ice into a drink. In particular, we had one specific question in mind: do quantum fluctuations speed up thermalisation, or slow down thermalisation?
How did we do it?
**This section is unavoidably a bit technical, so I've hidden it away. Click here to expand this section if you want the details!**
We used a theoretical technique known as the Keldysh formalism to study the dynamics of the p-spin model. This technique, proposed independently by Kadanoff and Baym as well as Keldysh, is based around the idea of a closed contour in time. Mathematically speaking, it’s a really elegant idea that allows use of the path integral approach to study the non-equilibrium dynamics of a physical system. Ultimately, for fully quantums spins this model is still too complex to solve in this manner and we must make an additional simplifying approximation known as the spherical approximation, which is a way of taking the quantum nature of the problem into account ‘on average’ (via a Lagrange multiplier) rather than attempting to treat the quantum problem fully exactly. At the end of the process, we end up with a series of three coupled differential equations which can be solved numerically (although as always, that statement drastically understates the amount of time it took me to code and test the entire procedure…!).
In order to perform a quench of the quantum fluctuations, we modify a parameter in the equation called \( \hbar \), which represents the Planck constant. This procedure is a little unusual - as the name suggests, the Planck constant is usually regarded as an immutable constant, like pi or the fine structure constant - but is ultimately well-defined: the \( \hbar \to 0 \) limit reproduces the classical equation of motion (which can be derived via a Martin-Siggia-Rose formalism using stochastic Langevin equation), while the case of \( \hbar > 0 \) represents the quantum system. In our case, to give us the freedom to change the strength of quantum fluctuations through the calculation, we make \( \hbar \) a time-dependent variable \( \hbar(t) \). This variable encodes all of the quantum behaviour of our system, ultimately appearing in only one single term of the resulting equations, and is responsible for all of the differences between the quantum case we consider, and the classical case previously studied by Cugliandolo et al.
In a real experiment, it isn’t possible to change Planck’s constant, but fear not - in real systems, it turns out that this is equivalent to changing a magnetic field, something which is much easier to do experimentally. (We address this in the Supplemental Material part of our paper.)
There was a further complication before we could continue, however. At the time when we began our study, no one had yet figured out the equations to allow us to start our simulation at a finite temperature: the initial state of our system was always an infinite temperature random state. While we began by studying this state, and the (unpublished) results were the same as the ones we’ll go on to look at below, ultimately we wanted to investigate states at much lower temperatures close to the spin glass transition, around \(k_B T \sim 1 \). A similar situation ,had been investigated by Cugliandolo et al. in classical glasses, where the equations to initialise the sytem at finite temperature (called TAP equations) could be computed, but in the quantum system they were not valid. (The same authors later derived a set of equations allowing exact initialisation of the quantum model at arbitrary temperatures, though to my knowledge no one has yet tried numerically simulating them: this would be a very interesting future step, and could confirm or refute our findings.)
To prepare our system at a finite temperature, we developed a novel ‘double quench’ numerical procedure where we first started our simulation at infinite temperature, then connected the system to an environment to allow it to cool down, then disconnected the system from its environment and performed a second quench. The way that we do this is, to my knowledge, unique, although around the same time that we developed this technique, Subir Sachdev’s group at Harvard used a similar approach to study the Sachdev-Ye-Kitaev model (which we have also investigated - hopefully that work will see the light of day eventually!). The key difference is that their initialisation step was performed by solving an imaginary-time Dyson equation rather than doing real-time evolution of the system coupled to a thermal bath; developing an imaginary-time method for the p-spin model, following the work of Cugliandolo et al., would be an extremely interesting extension of our work.
What did we find?
First, we checked that our computer code was able to reproduce known theoretical results - though not shown in our paper, we reproduced a very large number of previous works and made certain that our code performed well. After our equations and code passed all these checks, we were ready to use it to study quantum quenches of the isolated system, the main aim of our work.
Our central finding surprised us: we found that quenches which increased the strength of quantum fluctuations resulted in a slowing down of the dynamics, in stark contrast to the expectation based on previous studies of systems able to exchange energy with their environment.
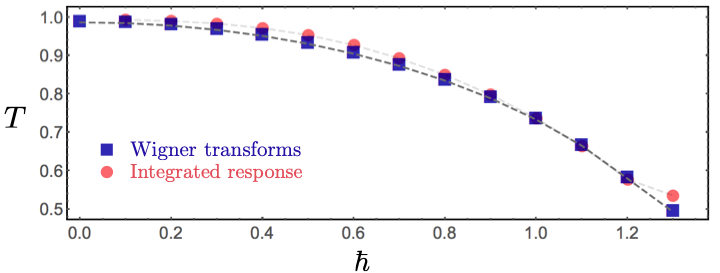
A plot showing the measured temperature T of the p-spin model, initially prepared at a temperature of T=1, following a sudden increase of quantum fluctuations (h). The temperature goes down as h is increased! (The temperature was computed using two different methods, as indicated in the figure, but the technical details aren’t important - what matters is that they agree.)
This result puzzled us for quite some time, and in fact we spent almost one entire (very stressful!) year checking and verifying it, looking for any bugs in the code or errors in the analysis. In the end, we found none. The result stood up to all scrutiny, and we searched for a way to explain it. (For a postdoc on a 2-year contract, the propect of spending this amount of time on a calculation that might not pan out is kind of terrifying, because it almost guarantees a difficult time securing further employment…!)
Ultimately, the explanation we found hinged on the concept of fluctuation-induced cooling, a means by which an isolated quantum system can decrease its effective temperature when quantum fluctuations are increased. This relies on the fact that the energy of the system is conserved. Loosely speaking, if we increase the strength of quantum fluctuations, then the temperature has to decrease accordingly in order for the total energy of the system to remain constant.

This plot shows the internal energy of the p-spin model (U) plotted against temperature T for four different values of the quantum fluctuation strength, here denoted by the Greek symbol Gamma. At a fixed internal energy U=-3, indicated by the blue dashed line, the system with Gamma=0.25 (for example) has a temperature of T=0.65. If we keep U fixed and increase Gamma to 0.75, this roughly corresponds to a system with energy T=0.55 - so increasing Gamma at fixed U has to result in a lower temperature!
Once we hit upon this, and verified it across a bunch of different mathematical and physical models of spin glasses, this explained everything that we were seeing! Like an awful lot of problems in physics, to paraphrase my PhD advisor, this turned out to be a case of “The answer is simple…once you know the answer!".
What’s next?
There are a number of ways forward for this result. First and foremost is the further testing and verification of this result in other theoretical - and even experimental - models. We’ve taken the first steps along this route by investigating the case of Ising spins, but were not able to fully investigate the dynamics of this model: this would be an interesting next step. Numerical simulations would also be useful: our small-scale exact diagonalisation tests (not shown in the main paper) could not reach large enough system sizes to be useful, as this model is extremely difficult to simulate. While testing our results, we also performed a number of additional checks, including adiabtic ramps (i.e. slow changes, rather than sudden ones), testing the stability of our results towards weak coupling to an environment (spoiler: the results are robust) and investigating several other forms of analysis which, given time, will hopefully see the light of day in another publication someday.
Long-term, though, the main thing I find interesting about our result is that idea that quantum fluctuations in isolated, disordered systems can enhance glassy behaviour and slow dynamics. This is reminiscent of quantum localisation effects seen in many-body localised systems, and suggests a possible connection between these two phenomena, despite their very different origins. Investigating that further will be the subject of some future work…watch this space!
Usual disclaimer: this post was written by me, not any of my colleagues or co-workers, and represents my views only. If you don’t like this post, blame me, not them! I should also add that our anonymous peer reviewers were extremely helpful and constructive despite a lengthy peer review process - my thanks to them for their patience and the improvements they suggested to the paper that ultimately enabled its publication in Physical Review Letters.
