When Randomness Meets Subatomic Precision
In 1960, Theodore Maiman and co-workers created the world’s first laser. Working on the principle of Light Amplification by Stimulated Emission of Radiation, the beam produced by a laser is unique in that all the photons in the beam have both the same wavelength and the same phase. Because of this innocuous-sounding property, the humble laser went on to change the world.

Top: waves with the same phase add together to make a bigger wave. Bottom: waves with exactly opposite phase cancel each other out entirely, leaving no wave.
In a normal light – say, a light bulb – the photons are produced over a range of wavelengths, and with random phase. Phase is important because when two waves with the same phase hit a detector – like your eye – they reinforce each other, add together and become brighter. When two waves with opposite phase hit the same point, they cancel each other out completely. In a regular light source like a light bulb, the waves are produced in a random mixture. In a laser, the beam is coherent and all the photons behave in precisely the same way, to the point where they are fundamentally indistinguishable from each other. You can see interference patterns in any type of wave, even including waves on a beach or those left by the wake of a boat – watch out for them the next time you’re at the seaside.
![Waves left in the wake of a boat. [Image from Wikimedia Commons]](/images/fjordn_surface_wave_boat.jpeg)
Waves left in the wake of a boat. [Image from Wikimedia Commons]
If you have a laser to hand in the form of a laser pointer or similar, then you can generate interference patterns yourself pretty easily. Just shine your laser through anything translucent, like a frosted glass window or a piece of sellotape. The beam coming out the other side will no longer be a focused, bright dot, but instead will be a blurry shifting pattern of light and dark regions that changes as you move the laser. This is known as a speckle pattern.

This is what I get if I shine my laser pointer through a frosted-glass door – a complicated pattern with bright and dark spots. Try it yourself!
What’s important here is that the pattern changes when you move the laser – running this logic in reverse, the precise form of the speckle pattern tells us something about where the laser is located. In particular, if we see the interference pattern change, we know that the laser has moved, and if we can reconstruct how far it has moved from how the pattern has changed, we can use the speckle pattern to make a highly precise measurement of length. Rather than changing the position of the laser, we could also change its wavelength and we’d see a similar effect – the interference pattern will change.
Interfering lasers to make precise measurements of length isn’t a new idea – it’s even what’s used in gravitational wave observatory LIGO to measure tiny changes in the lengths of the observatory’s 4km-long arms – but being able to work backwards from the speckle pattern to detect tiny changes in laser wavelength is less commonplace. Solving this problem has attracted attention in recent years due to its applications in new types of biomedical imaging, and a new piece of research just published this week from a team at my old alma mater the University of St Andrews (working with commercial company M Squared Lasers) has pushed the sensitivity of these measurements to unprecedented new levels.
The technical details can be found in the research paper, but in the simple terms that I understand it in, the team took a 5cm-wide hollow sphere with a highly reflective, yet rough coating on the inside (think white paint!), made a hole in it to shine a laser into, made another hole into it for the reflected light to get out of and then stuck a camera in front of the second hole to measure the emitted light.
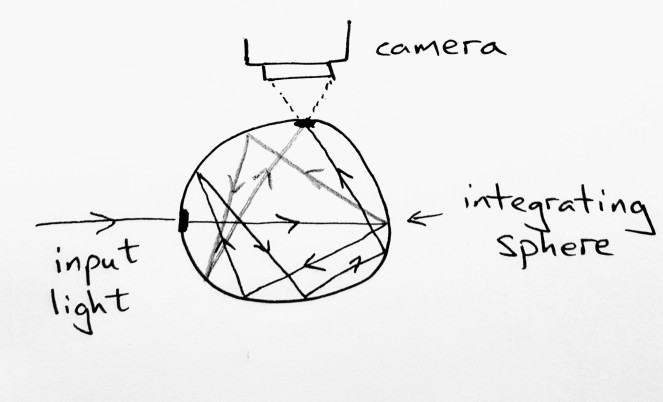
This is my (terrible) sketch of the experimental setup, showing what happens inside the integrating sphere. The light bounces around inside and splits into multiple trajectories. Eventually, they leave the sphere and are recorded on the camera. Waves with the same phase add together, leading to bright spots on the picture; waves with different phases subtract, leaving dark spots on the picture.
The hollowed-out sphere is properly called an ‘integrating sphere’, and turns out to be a particularly good way of scrambling up the light in such a way that the output is well and truly randomised. The light gets bounced all around the inside of the sphere before it finds its way out the exit. The emitted light is the result of the interference of a large number of different trajectories. The output beam no longer generates a coherent, pure dot of light but instead leads to a mottled ‘speckle’ pattern, just like we saw above.
![A real speckle pattern recorded by the team’s camera. [Image from the news release on the University of St Andrews School of Physics & Astronomy webpage.]](/images/speckle.png)
A real speckle pattern recorded by the team’s camera. [Image from the news release on the University of St Andrews School of Physics & Astronomy webpage.]
Decoding this highly complicated interference pattern, hopelessly scrambled though it may look, turns out to be the key to making extremely precise measurements. The pattern turns out to be extremely sensitive to laser parameters such as wavelength, with small changes in the latter leading to large changes in the former. By reconstructing the information locked away in this interference pattern and studying how it varies as the wavelength of the laser is changed, the team are able to measure changes in laser wavelength as small as one millionth the width of a typical atom. That’s about a millionth of a millionth the width of a typical full stop!
It goes without saying here that I’m somewhat glossing over the huge technical challenges involved in doing all of this accurately enough to accomplish their task – the analysis of the pattern is a hugely complex problem, and is the subject of most of the research paper (which is open access and freely available to anyone who wants further details).
But despite the complexity of the analysis, on the hardware side this new technology is comparatively smaller, simpler and easier to set up than the existing alternatives, not to mention being up to 100 times more accurate. This robustness of the hardware coupled with unrivalled accuracy of the measurements is good news for the development of future technologies. One particularly exciting application is its use in more accurate biomedical imaging. Additionally, probably sooner rather than later, it’s going to find its way into the measuring equipment used in research labs, as being able to very precisely measure tiny drifts in laser frequency will allow experimenters to quickly correct for them, enabling better control over experimental equipment and facilitating still more accurate measurements.
The humble laser has already been changing our world for nearly 60 years, but it looks like it’s not done yet.
Disclaimer: in the interests of transparency, I feel obliged to point out that I’ve previously worked with one of the authors of this new study, however I was not involved with this particular work. The information in this article is taken from the research paper and the associated press release.
